渲染中的球谐函数及Deringing

球谐函数(SH)¹，是一种相当有用的数学工具，在渲染领域应用很广，作为CubeMap的退化和补充，被大量用于低频光照表示。例如Unity的 light probe，UE4的 lightcache，以及一些不重要的实时光源，都可以用球谐光照快速的计算。球谐光照的优点是运行时的计算量与光源的数量无关，如果参数足够却可以较好的模拟实时的光照结果。

非专业入门一般推荐看这篇：[Stupid SH Tricks]²
实践可以看这篇，有代码：[SH: The gritty details]³

但这些货一般上来就给出个让人生畏的定义：

$$\scriptsize{Y_{\ell }^{m}(\theta ,\varphi )=(-1)^{m}{\sqrt {{(2\ell +1) \over 4\pi }{(\ell -m)! \over (\ell +m)!}}},P_{\ell }^{m}(\cos {\theta }),e^{im\varphi }}$$

[GI in Frostbite]⁴ 提供了一种新思路：隐函数⁵。
也仅限于概念上的推导，并不具备实践指导意义。

OK，我们从头开始：

基础知识

为了降低本文阅读门槛，加上这小节，大佬请略过。
数学语言组织不是很严谨，略过了一些非关键步骤及定义域处理。

> 内积

V上的内积就是一个函数，它把V中的元素的每个有序对$(u,v)$都映射为一个数字: $$\langle u, v \rangle = \int u(x)v(x)dx$$

内积是对点积的推广⁶。而点积是什么：投影
这里区别下卷积的定义，知乎有个形象的解释⁷： $$y(s) = \int_{0}^{s}u(\tau)h(s-\tau)d\tau$$

离散表达呢，就是函数的每个数字都一一相乘。另外，函数在matlab中其实也就是一组数字。

> 正交函数集与基函数

若n个函数$b_1(s),b_2(s),…,b_n(s)$构成一个函数集，当这些函数在区间(s1,s2)内满足： $$\small{\langle b_i, b_j \rangle = \int_{t_1}^{t_2}b_i(s)b_j(s)dt = \begin{cases}0 & i \neq j \\ K_i \neq 0 & i = j \end{cases}}$$
则此函数集为在区间(s1,s2)的正交函数集，当$K_i=1$，则为标准正交。

简单起见，下面的讨论均为标准正交。

如果不存在任何$b^{ * }(s)(≠0)$能满足正交条件：
$$\langle b_i, b^{ * } \rangle = 0, (i=1,2\cdots n)$$ 则称此函数集为区间(s1,s2)上的完备正交集。

由表示定理，信号f(s)可以被表示为这个完备正交函数集中各函数的线性组合: $f(s) = \sum_i c_i b_i$
其中 b 被称作基函数，c 可以通过内积得到：$c_i=\langle f,b_i\rangle$

> 最小二乘

那么，为什么可以通过内积运算得到系数c ?
来，上课：<最小二乘法本质⁷> & <理解特征函数⁸>

本质是个拟合问题，而拟合需要一个结果度量也就是能量函数，最小二乘是个不错的选择，我们定义： $$E(c)=\int (\sum_i c_i b_i(s) - f(s))^2 dt$$

求导，且由于 b 正交： $$\begin{aligned} \frac{\text{d}E}{\text{d}c_k} & =2\int (\sum_i c_i b_i(s) - f(s))b_k(s) dt \\ & = 2\int (c_k - f(s)b_k(s)) dt = 0 \\ & \Rightarrow c_k = \int f(s)b_k(s)dt = \langle f,b_k\rangle \end{aligned}$$

这同时也是帕塞瓦尔（Parseval）方程（等式）的推导过程。

> 欧拉-拉格朗日方程

简化自 <欧拉-拉格朗日方程推导>⁹

这里稍带点泛函，简述下思想，不然不好展开。
考察最速降线时间函数，将曲线看作路径f关于时间t的函数：
$$\begin{aligned} T[f] & = \int_{t_1}^{t_2} \frac{\sqrt{1+f^\prime(t)^2}}{\sqrt{2gf(t)}} dt \\ & \rightarrow \int_{x_1}^{x_2} L(x,f(x),f^\prime(x))dx \end{aligned}$$

很明显满足简单泛函形式，欧拉-拉格朗日方程(EL)就是对这类方程最优解问题的转化：

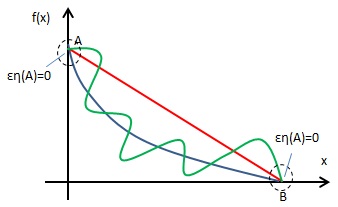
f0是最优函数，加入扰动函数εη(x)，η是满足端点处不扰动的任意函数，有点绕直接看公式： $$f(x,\epsilon) = (f_0+\epsilon \eta)(x),\eta(x_0)=0,\eta(x_1)=0$$

于是问题转换为关于ε的极值问题： $$\small{\begin{aligned} \frac{\text{d}A[\epsilon]}{\text{d}\epsilon} & =\int_{x_1}^{x_2} \frac{L(x,f(x,\epsilon),f'(x,\epsilon))}{d\epsilon} dx \\ & = \int_{x_1}^{x_2} \frac{\partial L}{\partial x}\frac{\partial x}{\partial \epsilon} + \frac{\partial L}{\partial f}\frac{\partial f}{\partial \epsilon} +\frac{\partial L}{\partial f'}\frac{\partial f'}{\partial \epsilon} dx \\ & \begin{cases}\frac{\partial x}{\partial \epsilon} = 0 \\ \frac{\partial f}{\partial \epsilon} = \frac{\partial (f_0+\epsilon \eta)}{\partial \epsilon} = \eta (x) \\ \frac{\partial f'}{\partial \epsilon} = \frac{\partial (f_0'+\epsilon \eta')}{\partial \epsilon} = \eta'(x) \end{cases} \\ & \Rrightarrow \frac{\text{d}A}{\text{d}\epsilon} = \int_{x_1}^{x_2}\frac{\partial L}{\partial f}\eta(x)dx+\int_{x_1}^{x_2}\frac{\partial L}{\partial f'}\eta'(x)dx \end{aligned}}$$

由分部积分及端点处η(x0)=0,η(x1)=0： $$\small{\begin{aligned} \frac{\text{d}A}{\text{d}\epsilon} & = \int_{x_1}^{x_2}\frac{\partial L}{\partial f}\eta(x)dx-\int_{x_1}^{x_2}(\frac{\partial L}{\partial f'})'\eta(x)dx \\ & = \int_{x_1}^{x_2}[\frac{\partial L}{\partial f}-\frac{\text{d}}{\text{d}x}(\frac{\partial L}{\partial f'})]\eta(x)dx \\ & \Rightarrow \frac{\partial L}{\partial f}-\frac{\text{d}}{\text{d}x}(\frac{\partial L}{\partial f'}) = 0 \end{aligned}}$$

即欧拉-拉格朗日方程(Euler-Lagrage equation)，可以帮助我们求解泛函下的极值，这里L是已知的。它的最初的思想来源于微积分中“可导的极值点一定是稳定点(临界点)”。它的思想在于：假定当前泛函的解已知，那么这个解必然使得泛函取得最小值（假定是最小值）。换言之，只要在泛函中加入任何扰动，都会使泛函的值变大，所以扰动为0的时候，就是泛函关于扰动的一个极小值。扰动用一个很小的数ε乘上一个连续函数η(x)。当ε趋近于0，意味着扰动也趋近于0。所以当扰动为0时，泛函对扰动程度的导数也为0。这就非常巧妙的把对函数求导转化成了一个单变量求导问题。

> 拉普拉斯方程

简化自 <调和映照漫谈 I-顾险峰>¹⁰

黎曼考察了这样一个物理问题：（Dirichlet问题）假设Ω是平面中的有界区域，由某种电阻率处处相同的材料制成。我们在Ω的边缘δΩ处设置电压g，问Ω内部电压函数u是多少？

根据物理定律，Ω内的电场诱导电流，电流发热做功，那么真实可能的电压函数必定使得发热功率最小。电流正比电压梯度，电阻率处处相同，因此电流发热功率可以表示成所谓的调和能量：

$$E(u)=\int_{\Omega}\langle \triangledown u, \triangledown u \rangle dA$$

如果u极小化调和能量，则称其为调和函数。

加入试探函数h，ε=0取得极值(上一节EL推导)：

$$\begin{aligned} \frac{\text{d}}{\text{d}\epsilon}\mid_{\epsilon=0} & = \int_{\Omega} \langle \triangledown u + \epsilon\triangledown h, \triangledown u + \epsilon\triangledown h \rangle dA \\ & = 2 \int_{\Omega} \langle \triangledown u, \triangledown h \rangle dA = 0 \end{aligned}$$

由分部积分： $$\small{\int_{\Omega} \langle \triangledown u, \triangledown h \rangle dA = \int_{\Omega} h \triangle u dA - \int_{\Omega} \triangledown \cdot (h \triangledown u)dA}$$

其中，由斯托克斯定理： $$\int_{\Omega} \triangledown \cdot (h \triangledown u)dA = \int_{\delta\Omega} h \triangledown u ds = 0$$

因为h任意，因此得到调和函数欧拉-拉格朗日方程: $$\begin{cases} \triangle u \equiv 0 \\ u\mid \delta \Omega = g \end{cases}$$

即所谓的Laplace方程。这里Laplace算子的物理意义是梯度的散度。事实上，热力学问题中稳衡温度场，弹性力学中橡皮膜的弹性位移，扩散过程中的化学浓度都是调和函数，都满足Laplace方程。满足拉普拉斯方程就意味着空间中没有“源”和“汇”。

PS：如何通俗理解拉普拉斯方程、泊松方程、亥姆霍兹方程¹¹

球谐函数的推导与性质

至于图形学为什么选用球谐，这点疑惑了很久，[stupid sh]²中给出了解释（大意就是用起来爽）：

Many of the uses in real-time graphics are just as a convenient way for representing spherical functions – visibility, lighting and reflectance. While there are many other basis functions that can be used, wavelets, wavelets on cube maps, spherical radial basis functions, and others.

OK，继续填坑：

> 勒让德方程及伴随勒让德方程

简化自 <分离变量法求解偏微分方程>¹²，<线性偏微分方程解法综述>¹³ … 个人理解，偏微分方程的分离变量法相当于c++的模版特化

勒让德方程是物理和工程领域里面常常遇到的一类常微分方程，也是拉普拉斯微分方程的一种变形，当试图在球坐标中求解三维拉普拉斯方程（或其他偏微分方程时），问题经常会归结为勒让德方程的求解。

首先是球面形式的拉普拉斯方程(等于零)： $$\scriptsize{{\frac {1}{r ^{2}}}{\frac {\partial }{\partial r }}\left(r ^{2}{\frac {\partial u}{\partial r}}\right)+{\frac {1}{r ^{2}\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial u}{\partial \theta }}\right)+{\frac {1}{r ^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}u}{\partial \varphi ^{2}}}}$$

上述偏微分方程u有多个自变量，无法直接进行求解，利用分离变量，分解为多个常微分方程：

引入：$u(r,\theta,\varphi) = R(r)Y(\theta,\varphi)$，
方程两边再乘以$r^2/YR$，再引入l(l+1)：

$$\scriptsize{\begin{aligned} & {\frac {1}{R ^{2}}}{\frac {\text{d}}{\text{d}r}}\left(r ^{2}{\frac {\partial R}{\partial r}}\right) + {\frac {1}{Y\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial Y}{\partial \theta }}\right)+{\frac {1}{Y\sin ^{2}\theta }}{\frac {\partial ^{2}Y}{\partial \varphi ^{2}}} \\ & \Rightarrow {\frac {1}{R}}{\frac {\text{d}}{\text{d}r}}\left(r ^{2}{\frac {\partial R}{\partial r}}\right) \\ & = -{\frac {1}{Y\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial Y}{\partial \theta }}\right)-{\frac {1}{Y\sin ^{2}\theta }}{\frac {\partial ^{2}Y}{\partial \varphi ^{2}}} = l(l+1) \end{aligned}}$$

$$\scriptsize{ \Rightarrow \begin{cases} (1){\frac {\text{d}}{\text{d}r}}\left(r ^{2}{\frac {\partial R}{\partial r}}\right) - l(l+1)R = 0 \\ (2){\frac {1}{\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial Y}{\partial \theta }}\right)+{\frac {1}{\sin ^{2}\theta }}{\frac {\partial ^{2}Y}{\partial \varphi ^{2}}} +l(l+1)Y=0 \end{cases}}$$

(1)为欧拉方程
(2)为球函数方程，所以只关乎角度部分。但(2)仍是偏微分方程，需要继续分离变量：

令：$Y(\theta,\varphi) = \Theta(\theta)\Phi(\varphi)$，
方程两边再乘以 $sin^2(\theta)/\Theta\Phi$，
同样引入 $m^2$ (其选取由本征值决定¹⁴)：

$$\scriptsize{\begin{aligned} & {\frac {sin\theta}{\Theta}}{\frac {\text{d} }{\text{d} \theta }}\left(\sin \theta {\frac {\text{d} \Phi}{\text{d} \theta }}\right) + {\frac {1}{\Phi}}\frac{\text{d}^2\Phi}{\text{d}\phi^2} + l(l+1)sin^2\theta = 0 \\ & \Rightarrow \\ & {\frac {sin\theta}{\Theta}}{\frac {\text{d} }{\text{d} \theta }}\left(\sin \theta {\frac {\text{d} \Phi}{\text{d} \theta }}\right) + l(l+1)sin^2\theta = -{\frac {1}{\Phi}}\frac{\text{d}^2\Phi}{\text{d}\phi^2} = m^2 \\ & \Rightarrow \begin{cases}(3)\frac{\text{d}^2\Phi}{\text{d}\phi^2} + m^2{\Phi} = 0 \\ (4){sin\theta}{\frac {\text{d} }{\text{d} \theta }}\left(\sin \theta {\frac {\text{d} \Phi}{\text{d} \theta }}\right) + [l(l+1)sin^2\theta - m^2]\Phi = 0 \end{cases}\end{aligned}}$$

到此，对(4)令 $x=cos\theta$，并记 $P(x) = \Theta(cos(\theta))$:

$$\scriptsize{(1-x^2),\frac{\text{d}^2,P}{\text{d}x^2} -2x\frac{\text{d} P}{\text{d}x} + \left(l[l+1] - \frac{m^2}{1-x^2}\right)P = 0}$$

这便是伴随勒让德多项式；
m=0时，即为勒让德微分方程。

> 勒让德多项式

当勒让德方程满足 |x|<1 时，可得有界解(解级数收敛)。可构成正交函数集，称为勒让德多项式：

$$P_n(x)=\frac{1}{2^n\cdot n!}\frac{\text{d}^n}{\text{d}x^n}[(x^2-1)^n]$$

伴随勒让德多项式(ALP)则有两个参数 l,m：

$$P^m_l(x)=(-1)^m(1-x^2)^{m/2}\frac{\text{d}^m}{\text{d}x^m}(P_l(x))$$

l,m分别是ALP的"order/band index"和"degree"。伴随勒让德多项式这一族正交多项式是分了很多"层"/“带"的，在每一个band l 里面， m 表示当前 band 的多项式元素下标。而且注意两个参数的取值范围：l>=0 ,m[0,l] 。这意味着前 n 个 band 总共有 n(n+1)/2 个多项式：

$$\begin{aligned} & P^0_0(x) \\ & P^0_1(x),P^1_1(x) \\ & P^0_2(x),P^1_2(x),P^2_2(x) \\ & \cdots \cdots \cdots \end{aligned}$$

一般我们都不会直接求解 $P^m_l(x)$ ,计算复杂度与重复度都很高，在高阶的情况（不能直接 hardcoded 了）时我们求解会用递推迭代的方法。几条足以求出所有ALP的递推式<注意这里是双阶乘>：

$$\small{\begin{aligned} & (l-m)P^m_l=x(2l-1)P^m_{l-1}-(l+m-1)P^m_{l-2} \\ & P^m_m=(-1)^m(2m-1)!!(1-x^2)^{m/2} \\ & P^m_{m+1}=x(2m+1)P^m_m \end{aligned}}$$

matlab里可以很方便的使用¹⁵

> 球谐函数

终于到正题，

球谐（基）函数是定义在球面上的。（下面球谐就简写为SH）。SH函数在通用情况下是在复数的基础上定义的，但是我们在图形学里面一般只关心定义在球面的实函数（在球谐光照里面，这个实函数可以是多通道的光强分布，也可以是传输函数，等等），所以这篇文章就只关心实球面调和(Real Spherical Harmonics)。

l 和 m 为什么是整数，因为他们是用来描述原子状态的不可再分的量子数。¹⁶

实球谐函数的解析式：[stupid sh]²

$$Y^m_l(\theta,\phi)= \begin{cases} \sqrt{2}K^m_l \cos(m\phi)P^m_l(\cos\theta) & (m>0) \\ \sqrt{2}K^m_l \sin(-m\phi)P^{-m}_l(cos\theta) & (m<0) \\ K^0_lP^0_l(cos\theta) & (m=0) \end{cases}$$

其中，P是上文的伴随勒让德多项式，K是归一化的缩放系数：

$$ K^m_l=\sqrt{\frac{2l+1}{4\pi}\cdot \frac{(l-|m|)!}{(l+|m|)!}} $$

注意，虽然 ALP 的 “degree” 参数 m 是非负整数，
但球谐函数的参数 m 则是可以取到负数的，取值区间关于0对称，即：

$$ l\in Z^*,m\in Z,m\in [-l,l] $$

> 性质

做个铺垫，先尝试计算下球谐的卷积，由标准正交不难得到（等效为点积）： $$\int _S \hat L(s) \hat t(s)ds=\sum ^{n^2} _{i=0}L_it_i$$

球谐光照(SH Lighting)分为下面几个阶段，

(离线)预计算传输 PRT(Precomputed Radiance Transfer)：Lighting Func和max(cos(theta), 0) transfer Func的卷积（即要求解的环境光照积分）正好可以压缩存贮为 Matrix4x4，对法线运算后重构环境光照。¹⁷
(离线)预计算辐照度 计算各采样点光强，存为lightcache
(实时)球谐旋转 篇幅过大，不展开，可以参考³¹⁶
(实时)辐照度的合成 lightcache之类，周边采样点融合
(实时)球谐向量点积得到着色颜色 辐照度的sh和PRT的sh进行点积

[其他性质]

快速收敛：针对处处光滑连续问题，SH basis的解快速收敛。这说明，像间接光照这样的低频问题(高频的问题可以用小波求解)，可在SH空间用极少的basis项去快速得到近似解(3 bands, 9 coefficients)
旋转不变性: 这保证了当环境光照发生相对旋转的时候，不出现计算结果的闪烁
分解：拟合拟合，具体参见[stupid sh]²
能量分布：L0表示平均亮度，其他层能量均0⁵
最大方向：L1三个系数即最大能量方向⁵

更多可参考 [gritty details]³

Deringing

简化自 [stupid sh]²

Deringing（振铃消除？）这词不太好翻译。
详细成因请自行百度，下面详细介绍消除方法：

> Windowing

常规方法是加窗：
为能可视化看到加窗的结果，这里只提供 Lanczos 窗¹⁸。球谐加窗的实现参考这篇¹⁹

%% 信号
% 信号参数
fs = 2500; %采样频率
N=fs*10;
t=(1:N)/fs;
w1=49.85*2*pi;
w2=w1+2*pi*1;
w3=w1-2*pi*1;
x = 10*cos(w1*t) + 0.005*cos(w2*t)+0.03*cos(w3*t);

%% 窗函数对信号频谱的影响
% 矩形窗
x1 = x;
MyPlotf=(0:(N-1))*fs/N;
FF1=fft(x1,N);
y1=abs(FF1)*2/N;%FFT幅值
y1(1)=y1(1)/2;
figure(3);
plot(MyPlotf,20*log10(y1));
xlim([40 60]);
title('rect win'); % 矩形窗后的频谱

% 汉宁窗
w = hanning (N,'periodic');
x2 = w'.*x;%加窗

FF2=fft(x2,N);
y2=abs(FF2)*2/N;%FFT幅值
y2(1)=y2(1)/2;
figure(4);
plot(MyPlotf,20*log10(y2));
xlim([40 60]);
title('hann win'); % 汉宁窗后的频谱

> Minimizing a Functinal

我们需要构造一组新的系数 g 满足：

由前文，投影拟合已经满足最小二乘，新函数应尽量贴近它
借助泛函思想，加入惩罚因子λ，使新构造函数曲率尽可能小

回顾下曲率的定义：$ \kappa ={\frac {|f''(x)|}{(1+f'{^2}(x))^{{3/2}}}} $ 可以发现，在梯度较小情况下，近似于二阶导，即拉普拉斯算子Δ。

于是，构造能量函数： $$\small{\begin{aligned} E(g) = \int (\tilde{f}(s) - f(s))^2ds +\lambda \int(\Delta \tilde{f}(s))^2ds \end{aligned}}$$

其中²⁰： $$\Delta \tilde{f}(s) = \sum_{l=1}^n \sum_{m=-1}^l l(l+1)g_l^m y_l^m$$

由正交性质不难得到： $$\small{\begin{aligned} E(g) = \sum_{l=1}^n \sum_{m=-1}^l ((g_l^m - c_l^m)^2 +\lambda l^2(l+1)^2 {g_l^m}^2)\end{aligned}}$$

极值处导数为零： $$\begin{aligned} \frac{\text{d}E}{\text{d}g_l^m} & = 2(g_l^m - c_l^m) +2\lambda l^2(l+1)^2 g_l^m = 0 \\ & \Rightarrow g_l^m = \frac{c_l^m}{1 + \lambda l^2(l+1)^2} \end{aligned}$$

上述方程中，如果λ=0，g 等于原始最小二乘的系数 c；如果λ无穷大，曲率将为零，意味着处处均匀。到此，还需要找到一个合适的λ，论文中给出的是指定曲率的解法。

求解，牛顿法：

首先，引入Ll 和 Bl，这部分可以预计算：

$$\begin{aligned} \Delta_{org}^2 & = \sum_{l=1}^n \sum_{m=-1}^l l^2(l+1)^2 {c_l^m}^2 \\ & = \sum_{l=1}^n l^2(l+1)^2 \sum_{m=-1}^l {c_l^m}^2 = \sum_{l=1}^n L_l B_l \end{aligned}$$

指定个目标值，由牛顿法： $$\begin{aligned} & \lambda_{n+1} = \lambda_{n} - \frac{f(\lambda_{n})}{f^\prime(\lambda_{n})} \\ & f(\lambda)=\Delta_{dst}^2-\sum_{l=1}^n\frac{L_l B_l}{(1+\lambda L_l)^2} \\ & f^\prime(\lambda)=2\sum_{l=1}^n\frac{L_l^2 B_l}{(1+\lambda L_l)^3} \end{aligned}$$

» 改进工作

可以发现加窗的方法需要进行FFT，离线采样还好，但在lightcache这种实时场景并不可取。因此，UE4实践了 [Minimizing a Functinal] 这套。具体做法是由美术指定一个相对合理的$Δ^2$，通过上小结方法强制将平均曲率缩减至一个较小对值。

但效果并不是很理想（不过比之Unity啥都没做，UE大法好）。实践发现$Δ^2$的变化范围还是比较大，固定参数并不能得到一个稳定结果，在照度变化大的地方尤其明显。对此将其改为原始平均曲率的倍数关系：

$$\Delta_{dst}^2 = \frac{\Delta_{org}^2}{\epsilon}$$

一般$ϵ=2.5$效果就很不错，
下面是UE4中实践的效果 <忽略图片质量>：

原始（未使用deringing） ringing_org UE4方法（最佳参数） ringing_ue4 我的改进方法（自适应） ringing_mine

最后

不自觉开了个大坑，总算填完了，
恶补了荒废许久的数理知识，收获不小。

Everything should be made as simple as possible, but no simpler.
Albert Einstein