写给程序员的量子计算基本原理

Quantum Supremacy

量子霸权，个人认为应译为量子优势。诸如此类，网上充斥着似懂非懂的科普。

本文将介绍量子计算的基本原理，量子比特，量子电路等概念。并通过一个简单的算法(Deutsch-Jozsa)来感受量子计算的优势与局限¹。

Qubit

类似经典计算机中的bit，量子计算机也会使用一些物理量来表示量子比特。

|0⟩ //量子0 (Ket 0)
|1⟩ //量子1 (Ket 1)

叠加态表示:

|x⟩ = a|0⟩ + b|1⟩

P(|0⟩) = a^2
P(|1⟩) = b^2
a^2 + b^2 = 1

|x⟩ = [a, b]^T //矩阵表示

多个量子比特：

|x⟩ = a|0⟩ + b|1⟩
|y⟩ = a|0⟩ + b|1⟩

|xy⟩ = ac|00⟩ + ad|01⟩ + bc|10⟩ + bd|11⟩
|xy⟩ = [ac, ad, bc, bd]^T //矩阵表示

Gate

经典计算机使用真值表来表示逻辑门的处理逻辑，量计算机则使用矩阵来表示量子逻辑门的功能。量子比特被处理时候，相当于施加矩阵乘法：

X Gate

img_gate_x

对 |0⟩ 施加 X：

$$ X|0⟩ = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \end{bmatrix} = |1⟩ $$

H Gate

img_gate_h

对 |0⟩ 施加 H：

$$ H|0⟩ = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ 1 \end{bmatrix} = \frac{1}{\sqrt{2}} |0⟩ + \frac{1}{\sqrt{2}} |1⟩ $$

即，50% |0⟩ or 50% |1⟩

可逆函数

在量子运算中，所有函数都要是可逆的，这里以与运算为例：

img_inv

通过此类方式，可构造可逆函数（是不是很神奇）。

Deutsch-Jozsa

未知函数 f:{0,1}→{0,1}，有以下两种性质之一，求具有哪一种：

Constant，输出一致：f(0) = 0，f(1) = 0 或 f(0) = 1，f(1) = 1
Balanced，输出平衡：f(0) = 0，f(1) = 1 或 f(0) = 1，f(1) = 0

可逆转换
如果 f 满足 Constant 时不可逆，需进行转换： $$ \begin{aligned} & f:(x) → f(x) \\ & U_f:(x,y) → (x,f(x))⊕y) \end{aligned} $$

构造以下电路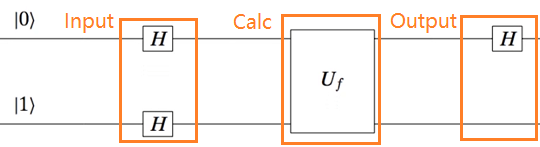： img_dj 1.Input
为了获得四种输入的叠加态引入两个 H 门： $$ \begin{aligned} & input = (\frac{1}{\sqrt{2}} |0⟩ + \frac{1}{\sqrt{2}} |1⟩)⊗(\frac{1}{\sqrt{2}} |0⟩ - \frac{1}{\sqrt{2}} |1⟩) \\ & = \frac{|00⟩ - |01⟩ + |10⟩ - |11⟩}{2} \end{aligned} $$

2.Calc
代入 $U_f:$|x y⟩ → |x (f(x)⊕y)⟩： $$ calc = \frac{U_f|00⟩ - U_f|01⟩ + U_f|10⟩ - U_f|11⟩}{2} $$

代入f(x)值：

Constant，f(0) = f(1) = 0：  
calc = 0.5(|00⟩ - |01⟩ + |10⟩ - |11⟩) =  H|0⟩H|1⟩  

Constant，f(0) = f(1) = 1：  
calc = 0.5(|01⟩ - |00⟩ + |11⟩ - |10⟩) = -H|0⟩H|1⟩  

Balanced，f(0) = 0，f(1) = 1：  
calc = 0.5(|00⟩ - |01⟩ + |11⟩ - |10⟩) =  H|1⟩H|1⟩  

Balanced，f(0) = 1，f(1) = 0：  
calc = 0.5(|01⟩ - |00⟩ + |11⟩ - |10⟩) = -H|1⟩H|0⟩

3. Output
从第一位不难看出，Constant:H|0⟩，Balanced:H|1⟩，利用H门性质：
$$ H(H|x⟩) = x => \begin{cases} H(H|0⟩) = 0 \\ H(H|1⟩) = 1 \end{cases} $$

也就是说，如果对第一个量子比特进行 H 门转换，Constant：0，Balanced：1

总结

虽然只调用了一次函数，通过使用叠加态量子比特，使函数对所有可能的输入都进行了处理。量子计算在观测之前，似乎是在对多种输入同时计算，但观测时候量子态会坍缩。并不能拿到所谓“并行计算”的所有输出。量子比特数量决定了吞吐量，需要对输出进行合并操作，有点类似map/reduce。并不是所有问题都适合用量子计算来解决，目前量子编程还停留在通过代码搭建量子电路的阶段，抽象程度较低。另一些更复杂有趣的算法这里就不展开了，学习可参考²。

附：硬件层

量子位数并不是粒子数量，而是纠缠量³。

实现分类⁴：

超导量子芯片
半导体量子芯片
2.1 基于电荷位置的量子比特
2.2 基于自旋的量子比特
2.3 半导体量子计算也正在从科研界转向工业界
其他类型体系的量子计算体系
3.1 离子阱量子计算
3.2 原子量子计算
3.3 核自旋量子计算
3.4 拓扑量子计算⁵⁶